Written by Sarthak Khillon

Description: Meet Swift Numerics: a new Swift package for computational mathematics. Take a tour of the protocols and types available in the package and find out how you can use them to write generic code. We'll also show you how and when to use the new Float16 type to improve performance and reduce memory usage. To get the most out of this session, you should have some familiarity with mathematics like logarithmic functions and real and imaginary numbers. You should also be familiar with generic programming in Swift. For more background, watch “Swift Generics (Expanded)” from WWDC18.

Swift Numerics Package Overview

• Provides building blocks for generic numerical computing in Swift.
• Includes a protocol called Real and a Complex number type.
• High-performance Float16 type.
• The package is open-source at github.com/apple/swift-numerics

Example: The Logit function

• This example uses the logit function from statistics.
• Essentially, given a probability p in the range 0...1, returns the log of the odds, log(p / (1 - p)).

You would implement the function like this:

import Darwin

func logit(_ p: Double) -> Double {
  log(p) - log1p(-p)
}

There's a small problem: this only supports Doubles. What about Floats or any other floating-point type? Our function should try to be generic.

A reasonable first attempt might look like:

import Darwin

func logit<T>(_ p: T) -> T {
  log(p) - log1p(-p)
}

But this won't compile because the log and log1p functions only make sense for a handful of floating-point types.

We need a constraint for our generic type. The Numerics module provides a Real protocol, which allows our code to work for any standard floating-point type, current or future. This code calls generic versions of the log and log1p functions.

import Numerics

func logit<NumberType: Real>(_ p: NumberType) -> NumberType {
  log(p) - log1p(-p)
}

The Real protocol

• Part of Swift Numerics package
• Provides generic access to all standard floating-point capabilities.

The definition is:

public protocol Real: FloatingPoint, AlgebraicField, RealFunctions { ... }

Note that AlgebraicField and RealFunctions are also new protocols defined in the Numerics package. However, Real is the one you should usually use.

Numeric Protocols in the Swift standard library

These are the protocols already defined in the Swift standard library:

This topic focuses on AdditiveArithmetic, SignedNumeric, and FloatingPoint

• AdditiveArithmetic applies to types that support addition and subtraction.
• SignedNumeric introduces multiplication.
• FloatingPoint adds many other operations for floating-point computation. This includes comparison functions, a way to decompose numbers into an exponent and significand, and useful constants like infinity or pi.

Protocols in the Numerics package

The Numerics package builds on protocols already in the Swift standard library.

• AlgebraicField augments SignedNumeric by introducing division and reciprocation.
• ElementaryFunctions augments AdditiveArithmetic by adding a large collection of common floating-point functions, such as logarithms and trigonometric functions.
  • RealFunctions extends ElementaryFunctions even further with some lesser-used functions, such as gamma and error functions.

The Real protocol combines all of these protocols into a single, unified concept:

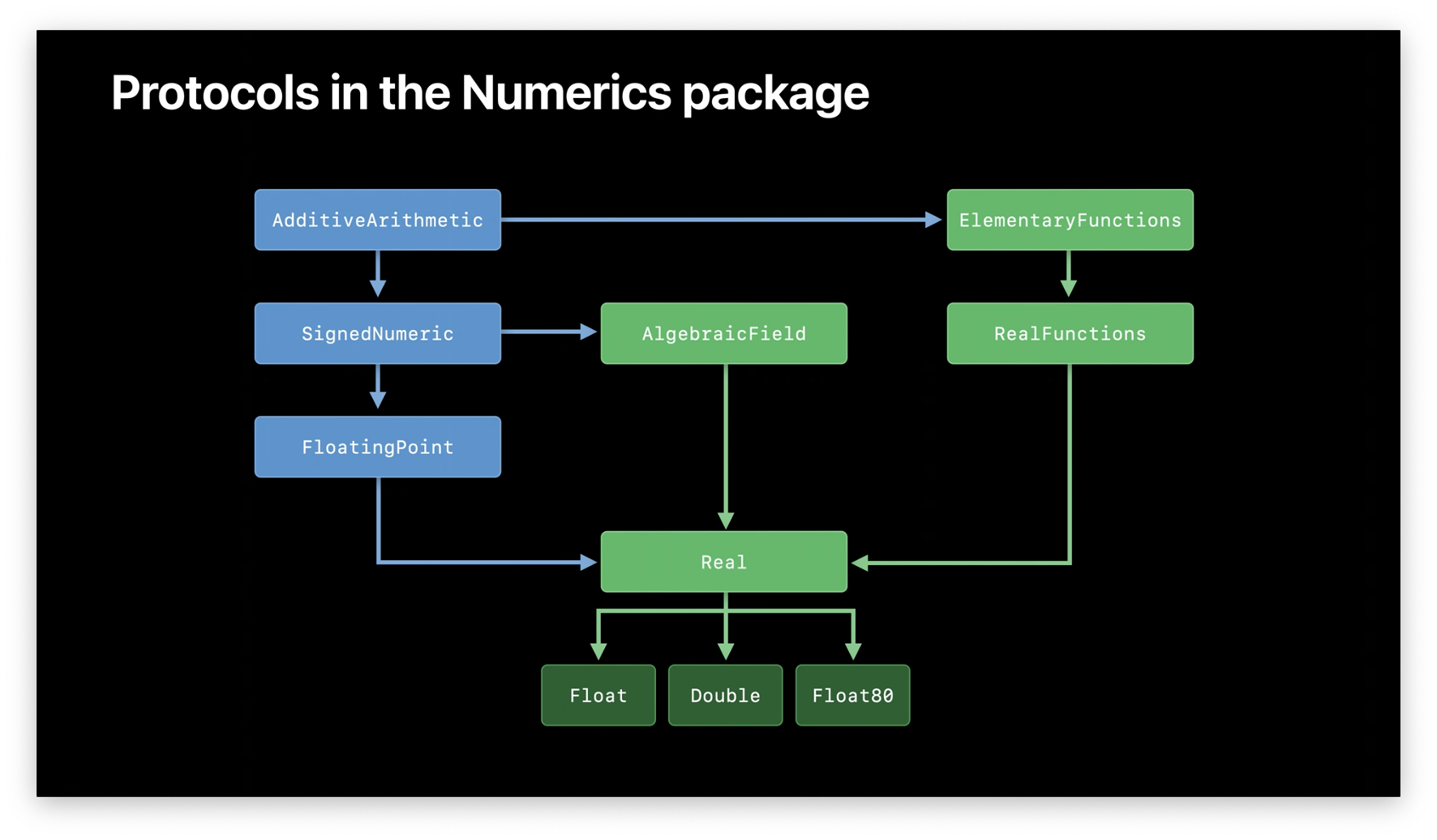
Implications of the Real protocol

• Generics constrained to Real support all standard floating-point types.
  • Reduces code duplication.
  • Simplifies maintenance.

• Makes defining new numerical types easier.

The Complex type

• Part of the Swift Numerics package
• Generic over any Real type, so it works for any floating-point type.

import Numerics

let z = Complex(1.0, 2.0)  // z = 1 + 2i

Complex defaults to Double, so the full type-annotated version of the code is:

import Numerics

let z: Complex<Double> = Complex(1.0, 2.0)  // z = 1 + 2i

Generic Numerical Programming

While Complex is a type by itself, it also enables generic numerical programming.

public struct Complex<NumberType> where NumberType: Real {
	/// The real component
	public var real: NumberType 

	/// The imaginary component
	public var imaginary: NumberType 

  /// Construct a complex number with specified real and imaginary parts
  public init (_ real: NumberType, imaginary: NumberType) { 
  	self.real = real 
  	self.imaginary = imaginary 
  }
}

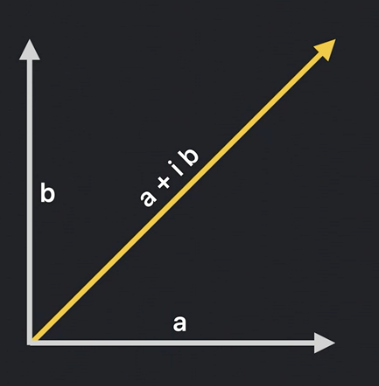
To make complex numbers fully functional, we need to extend them with the SignedNumeric protocol:

extension Complex: SignedNumeric {
	/// The sum of 'z' and 'w' 
  public static func +(z: Complex, w: Complex) -> Complex {
  	Complex(z.real + w.real, z.imaginary + w.imaginary) 
  }

  /// The difference of 'z' and ' w' 
  public static func -(z: Complex, w: Complex) -> Complex {
  	Complex (z.real - w.real, z.imaginary - w.imaginary) 
  }

  /// The product of 'z' and 
  public static func *(z: Complex, w: Complex) -> Complex { 
  	Complex(
  		z.real * w.real - z.imaginary * w.imaginary,
  		z.real * w.imaginary + z.imaginary * w.real
  	)
	}
}

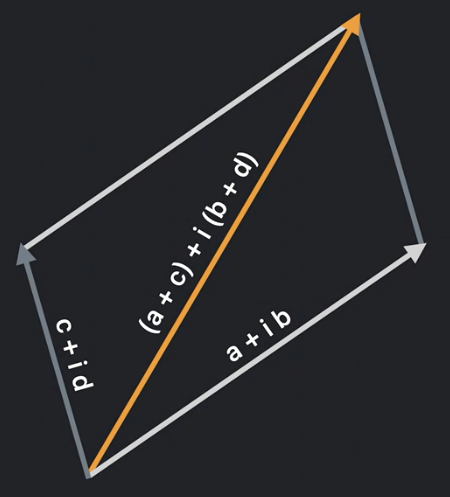
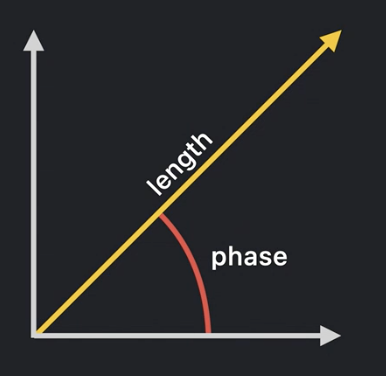
Complex numbers are often expressed in polar coordinates (length + phase angle):

extension Complex { 
  /// The Euclidean norm (a.k.a. 2-norm) of the number.
  public var length: NumberType { 
    .hypot(real, imaginary)
  } 

  /// The phase (angle, or "argument"). 
  ///
  /// Returns the angle (measured above the real axis) in radians. 
  public var phase: NumberType { 
  	.atan2(y: imaginary, x: real)
  }

  /// A complex value with specified polar coordinates.
  public init(length: Number Type, phase: Number Type) { 
  	self = Complex (.cos(phase), .sin(phase)).multiplied(by: length) 
  }
}

Compatibility with C and C++

Complex is a plain struct with 2 floating-point values, so its memory layout precisely matches the complex number types of C and C++. The following are all the same in memory:

• Complex<Double> (Swift)
• _Complex double (C)
• std::complex<double> (C++)

As a result, Swift code can exchange buffers of complex numbers with C/C++ APIs. You can just pass a pointer to a Swift Complex struct to a C/C++ library that also expects a complex type.

Example: Using Accelerate's BLAS functions

BLAS = Basic Linear Algebra Subroutines. Apple's implementation is written in C. Notice how the function accepts a pointer to the array of Complex<Double> numbers using the ampersand (&) operator.

import Numerics
import Accelerate

// Array of 100 random `Complex<Double>` numbers.
let z = (0 ..< 100).map {
  Complex(length: 1.0, phase: Double.random(in: -.pi ... .pi))
}

// Compute the Euclidean norm of `z`.
let norm = cblas_dznrm2(z.count, &z, 1)

One Caveat

The Numerics package treats complex infinity and NaN differently than in C or C++. This can affect code ported from C or C++.

However, Swift's treatment of these values is simpler and significantly more performant for multiplication and division. Below is a benchmark comparing Swift to C:

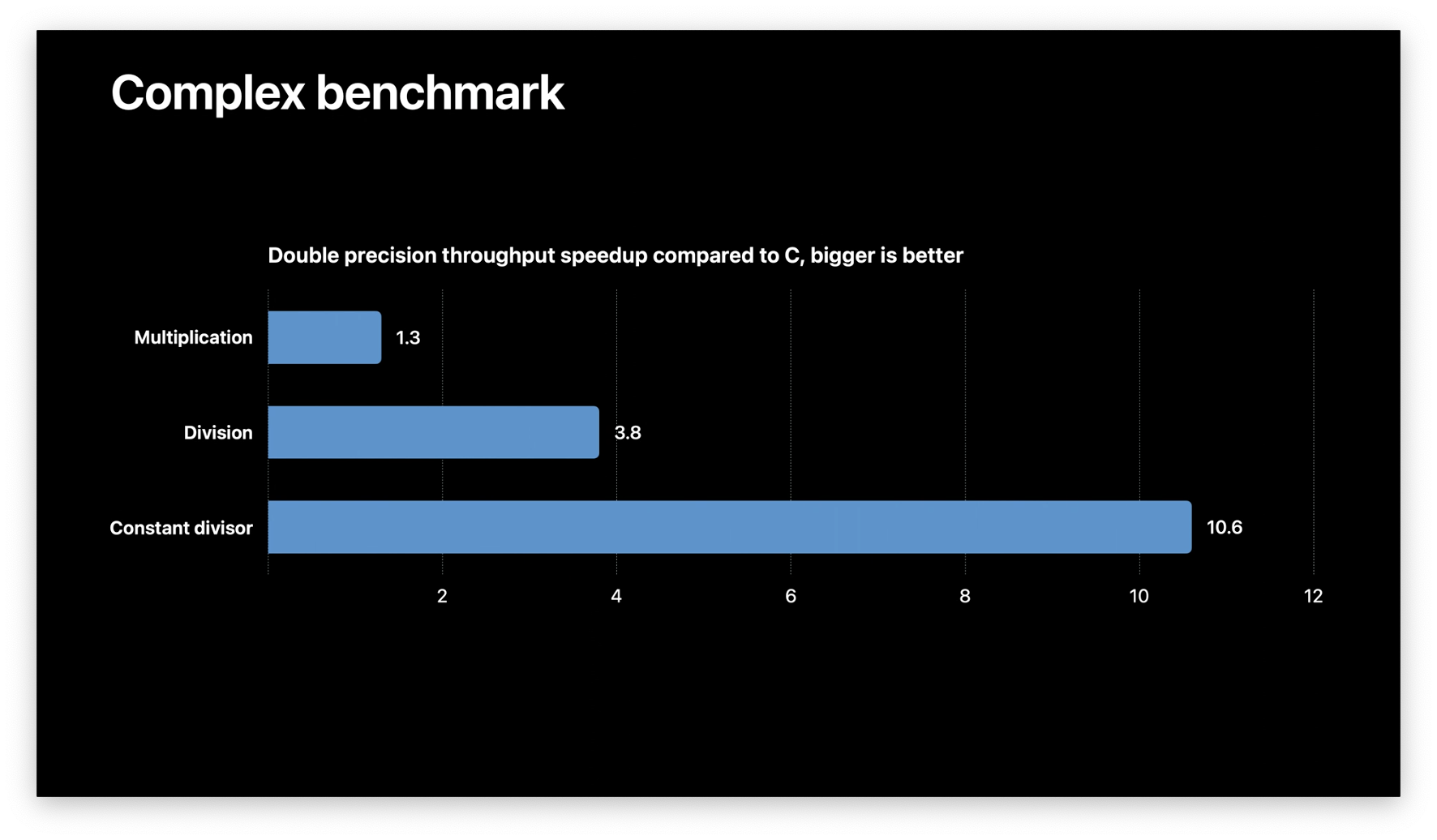
Numerics is a work in progress

Recent additions:

• Specialized handling for integer powers.
• Approximate equality.

Numerics is developed as a community on GitHub. Some of the projects being discussed include:

• Arbitrary-precision integers.
• Shaped arrays.
• Decimal floating point.

Float16

Is a new floating-point type in the Swift standard library.

• IEEE 754 standard format.
• Already available on iOS, iPadOS, tvOS, watchOS (ARM-based platforms).
• Calling convention for x86 is not yet finalized (working with Intel to fix this).

Is a normal floating-point type.

• Conforms to BinaryFloatingPoint and SIMDScalar.
• Conforms to Real from Swift Numerics.
• Supports all of the standard floating-point functions.

If you implement the Real protocol in your code, you will automatically get support for Float16.

Trade-offs

Pros:

• Significant performance gains because you can fit more of them into a SIMD register or a page of memory.
• Interoperates with C/Objective-C __fp16 type.

Cons:

• Low precision, small range.

Size and Constraints

Be mindful of these constraints when porting code that was originally written with Float or Double in mind:

Hardware Support

• Supported (and preferred) by Apple's GPUs.
• Supported by Apple's CPUs starting with A11 Bionic.
  • Scalar performance identical to Float or Double.
  • SIMD performance is 2x that of Float.
  • Float16 is simulated using Float operations on older hardware. The results are exactly the same, but without the speedup gains.

Here's a benchmark of Float16 against Float:

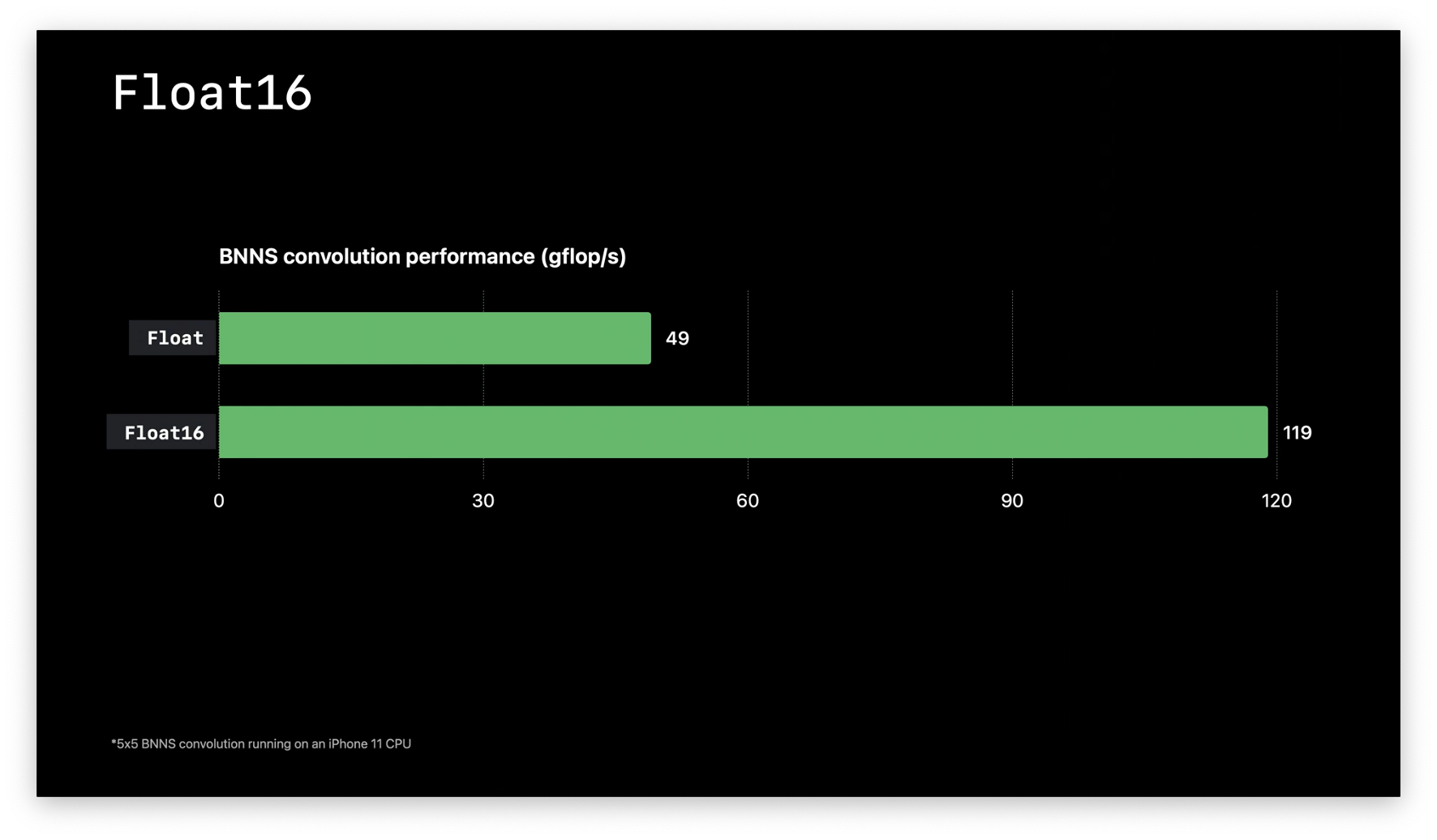
Getting involved with Swift Numerics

• Visit the GitHub page at github.com/apple/swift-numerics
• Participate in Swift forums under the category "Related Projects"